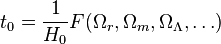Health and safety concerns - Sex Toys

Danish retailers report that they often lack information about the composition of sex toys that they sell. A recent (2006) study conducted by the Greenpeace Netherlands office found high level of phthalates in seven out of eight plastic sex toys tested.

Studies on rodents have revealed that when exposed to very large doses, phthalates can cause damage to the liver, lungs, kidneys, testes and can cause hormonal disruption. The latest research indicates that exposure to these substances can upset the body's ability to regulate hormone production, damage reproduction, and cause cause liver and kidney defects. They can also possibly cause cancer.

Sex toys are currently classified as novelties, despite their sexual nature. This is because sex toy manufacturers find the FDA (Food and Drug Administration) to have extensive testing and financial requirements for sex toys to be classified as medical devices. Therefore, sex toy manufacturers more often choose the less complex production by labeling them a novelty. Due to the novelty classification, sex toys are permitted to contain known toxins in them such as Phthalates (some of which have been banned in children’s toys by the CPSC) and in some cases lead paint.

In 2000, the development toward safe and nontoxic sex toys in the United States began with sexual health pioneers such as Lisa S. Lawless, Ph.D. whom founded one of the first retail sex toy stores (Holistic Wisdom) to carry only nontoxic sex toys. Her articles, radio and magazine interviews have been a major influence in the public eye; allowing consumers to become more aware of health concerns regarding sex toy safety. Lawless also began a movement toward safer sex toys through the National Association for the Advancement of Science & Art in Sexuality (NAASAS). This trade organization works with professionals in the field of sexuality and the adult industry to self regulate the safety of sex toys.

Age of the universe

The age of the universe is 13.75 ± 0.11 billion years (433.6 x 10¹⁵ seconds in SI units, or 13.75 Gigayears) within the Lambda-CDM concordance model. This is however only the estimated time since the Big Bang. It is not known if something existed before the singularity that we call Big Bang, nor if time is linear, since the expansion estimated by Hubble's law assumed a linear expansion, and later work indicates there may have been variations. The estimated changes in expansion are calculated to be both positive and negative, so Hubble and later estimates broadly agree.

The uncertainty range for the age of the universe has been obtained by the agreement of a number of scientific research projects. These projects included microwave background radiation measurements by Wilkinson Microwave Anisotropy Probe and other probes, and more ways to measure the expansion of the universe. Background radiation measurements give the cooling time of the universe since the Big Bang. Expansion of the universe measurements give accurate data to calculate the age of the universe.

Explanation

The Lambda-CDM concordance model describes the evolution of the universe from a very uniform, hot, dense primordial state to its present state over a span of about 13.75 billion years of cosmological time. This model is well understood theoretically and strongly supported by recent high-precision astronomical observations such as WMAP. In contrast, theories of the origin of the primordial state remain very speculative. If one extrapolates the Lambda-CDM model backward from the earliest well-understood state, it quickly (within a small fraction of a second) reaches a singularity called the "Big Bang singularity." This singularity is not considered to have any physical significance, but it is convenient to quote times measured "since the Big Bang" even though they do not correspond to a physically measurable time. For example, "10⁻⁶ second after the Big Bang" is a well-defined era in the universe's evolution. In one sense it would be more meaningful to refer to the same era as "13.7 billion years minus 10⁻⁶ seconds ago," but this is unworkable since the latter time interval is swamped by uncertainty in the former.

Though the universe might in theory have a longer history, the International Astronomical Union presently use "age of the universe" to mean the duration of the Lambda-CDM expansion, or equivalently the elapsed time since the Big Bang in the current observable universe.

Observational limits

Since the universe must be at least as old as the oldest thing in it, there are a number of observations which put a lower limit on the age of the universe; these include the temperature of the coolest white dwarfs, which gradually cool as they age, and the dimmest turnoff point of main sequence stars in clusters (lower-mass stars spend a greater amount of time on the main sequence, so the lowest-mass stars that have evolved off of the main sequence set a minimum age). On 23 April 2009 a gamma-ray burst was detected which was later confirmed to be over 13 billion years old.

Cosmological parameters

The age of the universe can be determined by measuring the Hubble constant today and extrapolating back in time with the observed value of density parameters (Ω). Before the discovery of dark energy, it was believed that the universe was matter-dominated, and so Ω on this graph corresponds to Ω_m. Note that the accelerating universe has the greatest age, while the Big Crunch universe has the smallest age.

The value of the age correction factor, F, is shown as a function of two cosmological parameters: the current fractional matter density Ω_m and cosmological constant density Ω_Λ. The best-fit values of these parameters are shown by the box in the upper left; the matter-dominated universe is shown by the star in the lower right.

The problem of determining the age of the universe is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the Universe is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. The fractional contribution of each to the current energy density of the Universe is given by the density parameters Ω_m, Ω_r, and Ω_Λ. The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter H₀ are the most important.

If one has accurate measurements of these parameters, then the age of the universe can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the Universe. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total age of the universe by integrating this formula. The age t₀ is then given by an expression of the form

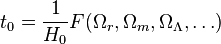
where the function F depends only on the fractional contribution to the universe's energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls that age of the universe, with a correction arising from the matter and energy content. So a rough estimate of the age of the universe comes from the inverse of the Hubble parameter,

To get a more accurate number, the correction factor F must be computed. In general this must be done numerically, and the results for a range of cosmological parameter values are shown in the figure. For the WMAP values (Ω_m, Ω_Λ) = (0.266, 0.732), shown by the box in the upper left corner of the figure, this correction factor is nearly one: F = 0.996. For a flat universe without any cosmological constant, shown by the star in the lower right corner, F = ²⁄₃ is much smaller and thus the universe is younger for a fixed value of the Hubble parameter. To make this figure, Ω_r is held constant (roughly equivalent to holding the CMB temperature constant) and the curvature density parameter is fixed by the value of the other three.

The Wilkinson Microwave Anisotropy Probe (WMAP) was instrumental in establishing an accurate age of the universe, though other measurements must be folded in to gain an accurate number. CMB measurements are very good at constraining the matter content Ω_m and curvature parameter Ω_k. It is not as sensitive to Ω_Λ directly, partly because the cosmological constant only becomes important at low redshift. The most accurate determinations of the Hubble parameter H₀ come from Type Ia supernovae. Combining these measurements leads to the generally accepted value for the age of the universe quoted above.

The cosmological constant makes the universe "older" for fixed values of the other parameters. This is significant, since before the cosmological constant became generally accepted, the Big Bang model had difficulty explaining why globular clusters in the Milky Way appeared to be far older than the age of the universe as calculated from the Hubble parameter and a matter-only universe. Introducing the cosmological constant allows the universe to be older than these clusters, as well as explaining other features that the matter-only cosmological model could not.

WMAP

NASA's Wilkinson Microwave Anisotropy Probe (WMAP) project's seven-year data release in 2010 estimated the age of the universe to be 1.375±0.011×10¹⁰ years (13.75 billion years old, with an uncertainty of plus or minus 110 million years).

However, this age is based on the assumption that the project's underlying model is correct; other methods of estimating the age of the universe could give different ages. Assuming an extra background of relativistic particles, for example, can enlarge the error bars of the WMAP constraint by one order of magnitude.

This measurement is made by using the location of the first acoustic peak in the microwave background power spectrum to determine the size of the decoupling surface (size of universe at the time of recombination). The light travel time to this surface (depending on the geometry used) yields a reliable age for the universe. Assuming the validity of the models used to determine this age, the residual accuracy yields a margin of error near one percent.

Currently, this is the value most quoted by astronomers.

Assumption of strong priors

Calculating the age of the universe is only accurate if the assumptions built into the models being used to estimate it are also accurate. This is referred to as strong priors and essentially involves stripping the potential errors in other parts of the model to render the accuracy of actual observational data directly into the concluded result. Although this is not a valid procedure in all contexts (as noted in the accompanying caveat: "based on the fact we have assumed the underlying model we used is correct"), the age given is thus accurate to the specified error (since this error represents the error in the instrument used to gather the raw data input into the model).

The age of the universe based on the "best fit" to WMAP data "only" is 13.75±0.13 Ga (the other estimate of 13.75±0.11 uses Gaussian priors based on earlier estimates from other studies). This number represents the first accurate "direct" measurement of the age of the universe (other methods typically involve Hubble's law and age of the oldest stars in globular clusters, etc.). It is possible to use different methods for determining the same parameter (in this case – the age of the universe) and arrive at different answers with no overlap in the "errors". To best avoid the problem, it is common to show two sets of uncertainties; one related to the actual measurement and the other related to the systematic errors of the model being used.

An important component to the analysis of data used to determine the age of the universe (e.g. from WMAP) therefore is to use a Bayesian Statistical analysis, which normalizes the results based upon the priors (i.e. the model). This quantifies any uncertainty in the accuracy of a measurement due to a particular model used.

History

In the 18th century, the concept that the age of the Earth was millions, if not billions, of years old began to be realized. However, most scientists throughout the 19th century and into the first decades of the 20th century presumed that everything else in the Universe was Steady State and eternal, with maybe stars coming and going but no changes occurring at the largest scale known at the time.

The first scientific theories indicating that the age of the Universe might be finite were the studies of thermodynamics, formalized in the mid 19th century. The concept of entropy dictates that if the Universe (or any other closed system) were infinitely old then everything inside would be at the same temperature, and thus there would be no stars and no life. No scientific explanation for this contradiction was put forth at the time. In 1915 Albert Einstein published the theory of general relativity. This theory clearly showed that the Universe cannot be static and must be either expanding or contracting. Einstein himself did not believe this result and so he added what he called a cosmological constant to his equations in an unsuccessful attempt to produce a theory consistent with a Steady State Universe.

The first direct observational evidence that the Universe has a finite age came from the observations of astronomer Edwin Hubble published in 1929. Earlier in the 20th century, Hubble and others resolved individual stars within certain nebula thus determining that they were galaxies, similar to, but external to, our Milky Way Galaxy. In addition, these galaxies were very large and very far away. Spectra taken of these distant galaxies showed a red shift in their spectral lines presumably caused by the Doppler effect, thus indicating that these galaxies were speeding away from the Earth. In addition, the further away these galaxies seemed to be, the greater the redshift and thus the faster they seemed to be speeding away. This was the first direct evidence that the Universe is not static but expanding. By calculating when all of the objects must have started speeding out from the same point yielded the first estimate of the age of the Universe. Hubble's initial value for age was very low as the galaxies were assumed to be much closer than later observations found them to be.

The first reasonably accurate measurement of the rate of expansion of the Universe, a numerical value now known as the Hubble constant, was made in 1958 by astronomer Allan Sandage. His measured value for the Hubble constant yielded the first good estimate of the age of the Universe, coming very close to the value range generally accepted today.

However Sandage, like Einstein, did not believe his own results at the time of discovery. His value for the age of the Universe was too short to reconcile with the 25 billion year age estimated at that time for the oldest known stars. Sandage and other astronomers repeated these measurements numerous times, attempting to reduce the Hubble constant and thus increase the resulting age for the Universe. Sandage even proposed new theories of cosmogony to explain this discrepancy. This issue was finally resolved by improvements in the theoretical models used for estimating the ages of stars. Presently, using these new models for stellar evolution, the estimated age of the oldest known star is about 13.2 billion years.

The discovery of microwave cosmic background radiation announced in 1965 finally brought an effective end to the remaining scientific uncertainty over the expanding Universe. The space probe WMAP, launched in 2001, produced data that determines the Hubble constant and the age of the Universe independent of galaxy distances, removing the largest source of error.